問題
次の文章の$\boxed{ }$内に、選択肢の中から最も適したものを選び、その番号を記せ。
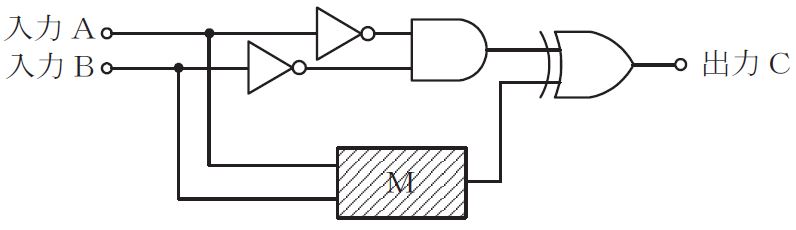
図4に示す論理回路において、$M$の論理素子が$\boxed{ }$であるとき、入力$A$及び$B$から出力$C$の論理式を求め変形し、簡単にすると、$\small{C} = \small{A} \cdot \small{B} + \overline{\small{A}} \cdot \overline{\small{B}}$で表される。

解答 4
AND回路の出力をABとすると、以下の真理値表ができる。
| A | B | AB | M | C |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 1 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 1 |
出力ABと出力Mの排他的論理路が、上の真理値表の出力Cのようになるので、以下の真理値表ができる。
| A | B | AB | M | C |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
この真理値表より、A, Bを入力して出力Mになるような論理素子は④AND回路となる。

