問題
次の文章の$\boxed{ }$内に、選択肢の中から最も適したものを選び、その番号を記せ。
面積Aの金属板2枚を間隔$d$だけ隔てて平行に置き、その間を誘電率$\epsilon$の誘電体で満たした並行板コンデンサがある。このコンデンサの静電容量を$C$とすると、これらの間には$C = \boxed{ }$の関係がある。
| ① | $\epsilon d A$ |
| ② | $\frac{\epsilon A}{d}$ |
| ③ | $\frac{\epsilon d}{A}$ |
| ④ | $\frac{A}{\epsilon d}$ |
| ⑤ | $\frac{d}{\epsilon A}$ |
解答 2
コンデンサ
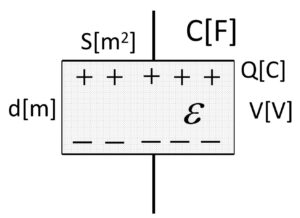
極板間の電圧:V[V]
極板間の誘電率:$\epsilon$
極板の面積:$S[m^2]$
2つの極板間の距離:$d[m]$
上図のようなコンデンサがある。
以下の関係式が成り立つ。
$Q = CV [C]$
ここで、$C$は静電容量と呼ばれるもので、以下のようになる。
$C = \epsilon \frac{S}{d}[F]$
また、コンデンサに蓄えられる静電エネルギーは以下になる。
$W = \frac{1}{2} C V^2[J]$

