問題
次の文章の$\boxed{ }$内に、選択肢の中から最も適したものを選び、その番号を記せ。
図1~図5に示すベン図において、A、B及びCが、それぞれの円の内部を表すとき、斜線部分を示す論理式が$\scriptsize{} \overline{\scriptsize{A} \cdot \scriptsize{C}} \cdot \scriptsize{B} + \overline{\scriptsize{A} \cdot \scriptsize{B}} \cdot \scriptsize{C}$と表すことができるベン図は、$\boxed{ }$である。
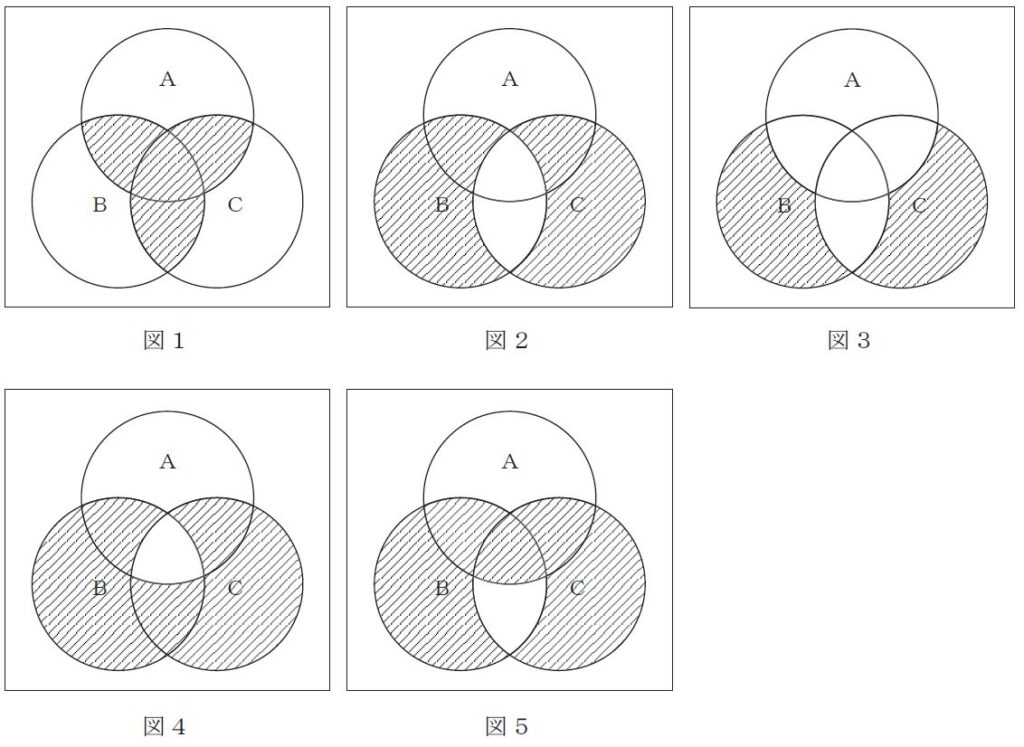
| ① | 図1 |
| ② | 図2 |
| ③ | 図3 |
| ④ | 図4 |
| ⑤ | 図5 |
解答 4
$\scriptsize{} \overline{\scriptsize{A} \cdot \scriptsize{C}} \cdot \scriptsize{B} + \overline{\scriptsize{A} \cdot \scriptsize{B}} \cdot \scriptsize{C}$のカルノー図を描くと以下となる。
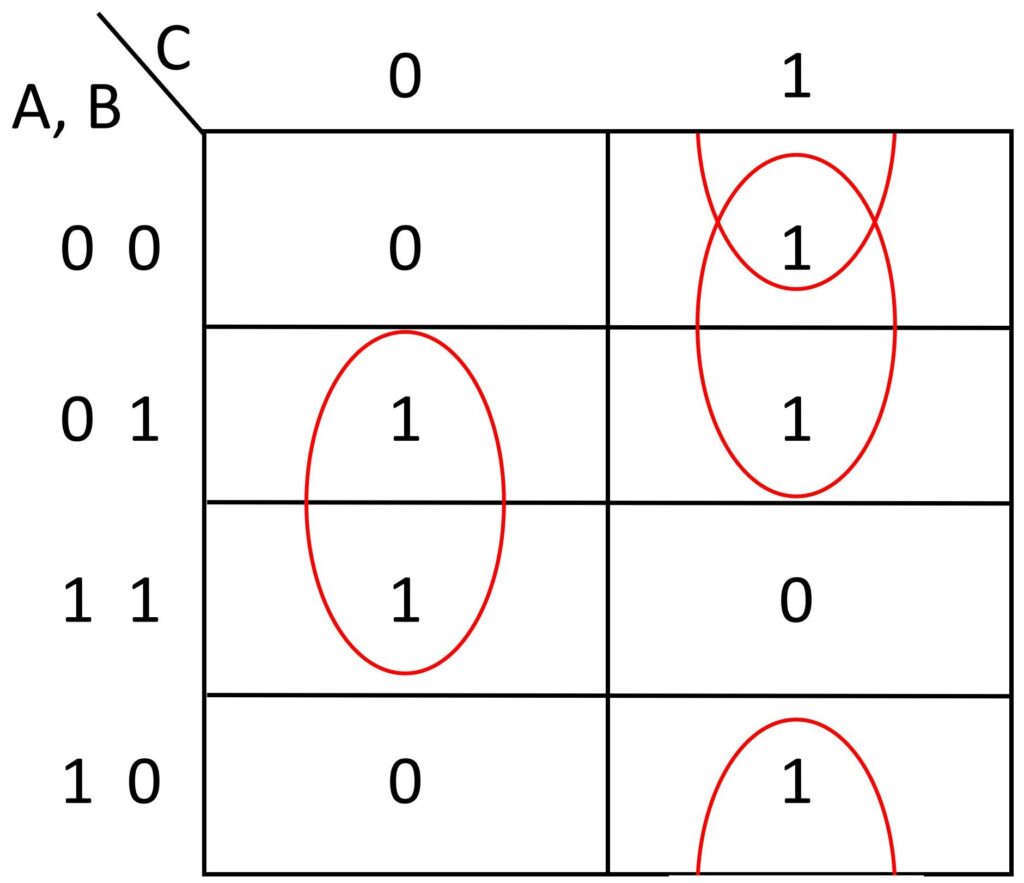
カルノー図より、以下の論理式が導ける。
$$\scriptsize{} \scriptsize{B} \cdot \overline{\scriptsize{C}} + \overline{\scriptsize{B}} \cdot \scriptsize{C} + \overline{\scriptsize{A}} \cdot \scriptsize{C}$$
ここで、$\scriptsize{} \scriptsize{B} \cdot \overline{\scriptsize{C}} + \overline{\scriptsize{B}} \cdot \scriptsize{C}$は、BとCの排他的論理和を表す。
あとは、$\scriptsize{} \overline{\scriptsize{A}} \cdot \scriptsize{C}$を加えれば、図4のようになる。

