問題
次の流れ図は、10進整数 j(0 < j < 100)を8桁の2進数に変換する処理を表している。2進数は下位桁から順に、配列の要素NISHIN(1)からNISHIN(8)に格納される。流れ図のa及びbに入れる処理はどれか。ここで、j div 2はjを2で割った商の整数部分を、j mod 2は j を2で割った余りを表す。
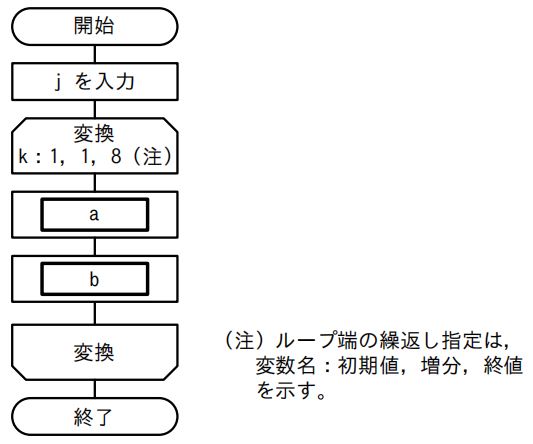
| a | b | |
| ア | j ← j div 2 | NISHIN(k) ← j mod 2 |
| イ | j ← j mod 2 | NISHIN(k) ← j div 2 |
| ウ | NISHIN(k)← j div 2 | j ← j mod 2 |
| エ | NISHIN(k)← j mod 2 | j ← j div 2 |
解答 エ
[a]
まず、j を2で割ったあまりを2進数配列要素NISHIN(k)に格納します。
[b]
次の計算のために、jには2で割った商を代入します。
10進数から2進数への変換は、10進数nに対して2で割った余りを順に下位ビットから並べていけば求まります。
例として、10進数n = 23の場合を示します。
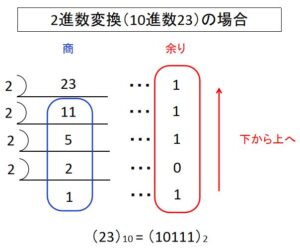
10進数23を2進数にすると、(10111)2が求まりました。
.jpg)
